
어때요, 여러분! 혹시 "양자"라는 단어만 들어도 머리가 🤯 핑 도는 분들 계신가요? 걱정 마세요! 양자역학은 알면 알수록 신기하고 재밌는 세계랍니다. 특히 양자 중첩은 양자컴퓨팅의 핵심 원리이기도 하고, SF 영화에 자주 등장하는 소재이기도 하죠. 지금 이 글을 읽지 않으면 양자 세계의 짜릿한 재미를 놓칠지도 몰라요! 😱 자, 그럼 양자 중첩의 세계로 함께 떠나볼까요? 🚀
오늘 우리가 함께 알아볼 내용은 바로 이거예요! 👇
- 양자 중첩이란 무엇이며, 왜 중요할까요? 🤔
- 슈뢰딩거의 고양이는 왜 유명할까요? 🐱
- 양자 중첩은 양자 컴퓨팅에 어떻게 활용될까요? 💻
양자 중첩, 그게 뭔데요? 🧐
양자 중첩은 쉽게 말해 하나의 양자 시스템이 동시에 여러 상태로 존재하는 것을 의미해요. 마치 동전이 던져지기 전에는 앞면도 뒷면도 아닌 상태로 존재하는 것과 비슷하죠. 🪙 양자 세계에서는 전자가 동시에 여러 위치에 존재하거나, 스핀이 위쪽 방향과 아래쪽 방향을 동시에 가질 수 있답니다. 정말 신기하죠? 🤩
이런 중첩 상태는 우리가 관측하는 순간 하나의 상태로 확정돼요. 동전을 던져서 앞면이 나오거나 뒷면이 나오는 것처럼요. 🫨 양자 중첩은 양자역학의 핵심 원리 중 하나이며, 양자 컴퓨팅, 양자 통신 등 다양한 분야에 응용되고 있어요.
슈뢰딩거의 고양이, 살아있을까 죽어있을까? 🐈⬛

슈뢰딩거의 고양이는 양자 중첩의 개념을 설명하기 위해 에르빈 슈뢰딩거가 제시한 사고 실험이에요. 밀폐된 상자 안에 고양이, 독극물 병, 방사성 원자, 그리고 방사성 원자가 붕괴하면 독극물 병을 깨뜨리는 장치를 넣어두는 거죠. 🧪
방사성 원자가 붕괴할 확률은 50%예요. 따라서 상자를 열기 전까지 고양이는 살아있는 상태와 죽어있는 상태가 중첩된 상태로 존재한다고 볼 수 있어요. 🤯 물론 현실에서는 말이 안 되지만, 양자 중첩의 기묘함을 잘 보여주는 예시랍니다.
| 구분 | 설명 |
|---|---|
| 슈뢰딩거의 고양이 | 밀폐된 상자 안의 고양이는 상자를 열기 전까지 살아있는 상태와 죽어있는 상태가 중첩되어 존재한다는 사고 실험. 양자 중첩의 개념을 시각적으로 보여주는 예시. |
| 양자 중첩 | 양자 시스템이 동시에 여러 상태로 존재하는 현상. 전자가 여러 위치에 동시에 존재하거나, 스핀이 위쪽 방향과 아래쪽 방향을 동시에 가질 수 있음. |
양자 중첩, 양자 컴퓨팅의 핵심 열쇠 🔑
양자 컴퓨팅은 양자역학의 원리를 이용하여 기존 컴퓨터보다 훨씬 빠른 속도로 복잡한 문제를 해결할 수 있는 기술이에요. 여기서 양자 중첩은 양자 컴퓨터의 기본 단위인 큐비트(qubit) 가 0과 1의 상태를 동시에 가질 수 있도록 해주는 핵심적인 역할을 해요. 💻
기존 컴퓨터의 비트(bit)는 0 또는 1의 값만 가질 수 있지만, 큐비트는 양자 중첩을 통해 0과 1의 상태를 동시에 표현할 수 있기 때문에 훨씬 많은 정보를 처리할 수 있답니다. 덕분에 양자 컴퓨터는 신약 개발, 금융 모델링, 인공지능 등 다양한 분야에서 혁신을 가져올 것으로 기대되고 있어요. 🚀
선형 대수, 양자 중첩 이해의 기초 다지기 🧮

양자 중첩을 제대로 이해하려면 선형 대수의 기본적인 개념을 알아두는 것이 좋아요. 선형 대수는 벡터, 행렬, 선형 변환 등을 다루는 학문인데, 양자 상태를 수학적으로 표현하고 계산하는 데 필수적인 도구랍니다. 🤓
예를 들어, 양자 상태는 벡터로 표현할 수 있고, 양자 연산은 행렬로 표현할 수 있어요. 선형 대수를 배우면 양자 중첩을 더 깊이 이해하고, 양자 알고리즘을 설계하는 데도 도움이 될 거예요. 📚
확률적 해석, 불확실성을 받아들이기 🤝
양자역학은 본질적으로 확률적인 이론이에요. 즉, 어떤 양자 시스템의 상태를 정확하게 예측하는 것은 불가능하며, 단지 확률적으로만 예측할 수 있을 뿐이죠. 😥 양자 중첩 역시 확률적인 현상이기 때문에, 결과를 정확하게 예측하는 것은 불가능해요.
하지만 이러한 불확실성을 받아들이고 확률적인 해석을 통해 양자 시스템을 이해하는 것이 중요해요. 확률적 해석은 양자역학을 이해하는 데 필수적인 요소이며, 양자 기술을 개발하는 데도 중요한 역할을 한답니다. 💡
양자 계산, 무한한 가능성의 세계로! 🌌
양자 중첩을 이용한 양자 계산은 기존 컴퓨터로는 풀기 어려웠던 문제들을 해결할 수 있는 새로운 가능성을 제시해요. 예를 들어, 양자 컴퓨터는 거대한 데이터베이스에서 원하는 정보를 훨씬 빠르게 검색할 수 있고, 복잡한 화학 반응을 시뮬레이션하여 신약 개발에 기여할 수 있어요. 🧪
물론 아직 양자 컴퓨터는 개발 초기 단계에 있지만, 앞으로 양자 기술이 발전하면 우리 사회에 엄청난 변화를 가져올 것으로 기대돼요. 양자 계산은 무한한 가능성을 가진 미래 기술이며, 우리 모두가 관심을 가져야 할 분야랍니다. ✨
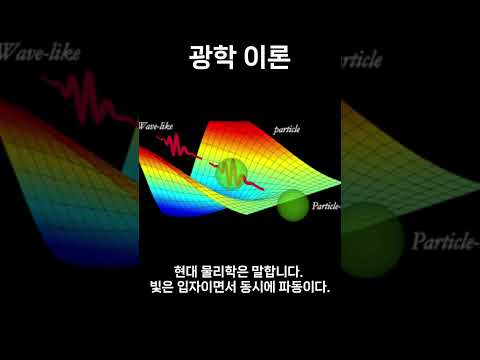
양자 광학, 빛으로 정보를 다루다 🔆
양자 광학은 빛의 양자적인 성질을 연구하는 학문이에요. 빛은 입자이면서 동시에 파동의 성질을 가지고 있는데, 이러한 빛의 이중성은 양자역학의 핵심 개념 중 하나인 파동-입자 이중성을 잘 보여준답니다. 🌊
양자 광학에서는 빛의 양자 상태를 이용하여 정보를 처리하고 전송하는 기술을 연구해요. 예를 들어, 양자 암호 통신은 빛의 양자 상태를 이용하여 해킹이 불가능한 안전한 통신을 구현할 수 있어요. 🔒 양자 광학은 양자 기술의 중요한 분야이며, 앞으로 더욱 발전할 것으로 기대됩니다.
양자 얽힘, 신기한 연결고리 🔗
양자 얽힘은 두 개 이상의 양자 시스템이 서로 밀접하게 연결되어 있어서, 하나의 상태를 측정하면 다른 상태가 즉시 결정되는 현상이에요. 마치 두 개의 동전이 얽혀 있어서, 하나를 던져서 앞면이 나오면 다른 하나는 무조건 뒷면이 나오는 것과 같죠. 🪙
양자 얽힘은 양자 통신, 양자 암호, 양자 컴퓨팅 등 다양한 분야에 응용될 수 있어요. 특히 양자 얽힘을 이용하면 정보를 빛보다 빠르게 전송할 수 있다는 주장이 있지만, 아직까지는 이론적인 가능성만 제시되고 있답니다. 🤔
양자 텔레포테이션, 순간 이동이 가능할까? teleportation 💫
양자 텔레포테이션은 양자 얽힘을 이용하여 양자 상태를 한 곳에서 다른 곳으로 전송하는 기술이에요. 여기서 중요한 점은 물질 자체가 이동하는 것이 아니라, 양자 상태에 담긴 정보만 이동한다는 것이죠. 🚀
양자 텔레포테이션은 양자 통신, 양자 암호 등 다양한 분야에 응용될 수 있지만, 아직까지는 실험실 수준에서만 구현되고 있답니다. 미래에는 양자 텔레포테이션 기술이 발전하여 SF 영화에서 보던 순간 이동이 가능해질지도 몰라요! 🤩
양자 센서, 세상을 더 정밀하게 감지하다 📡
양자 센서는 양자역학의 원리를 이용하여 기존 센서보다 훨씬 정밀하게 물리량을 측정할 수 있는 센서예요. 예를 들어, 양자 센서는 자기장, 중력, 온도, 압력 등을 매우 정확하게 측정할 수 있어요. 🌡️
양자 센서는 의료, 환경 모니터링, 국방 등 다양한 분야에 응용될 수 있어요. 예를 들어, 양자 센서를 이용하면 뇌파를 더 정확하게 측정하여 뇌 질환을 진단하거나, 지하 자원을 더 효율적으로 탐사할 수 있어요. 🔍
양자 시뮬레이션, 복잡한 현상을 예측하다 🔮
양자 시뮬레이션은 양자 컴퓨터를 이용하여 복잡한 물리 현상이나 화학 반응을 시뮬레이션하는 기술이에요. 기존 컴퓨터로는 시뮬레이션하기 어려웠던 복잡한 문제들을 양자 컴퓨터를 이용하면 훨씬 빠르고 정확하게 해결할 수 있답니다. 💻
양자 시뮬레이션은 신약 개발, 신소재 개발, 에너지 기술 개발 등 다양한 분야에 응용될 수 있어요. 예를 들어, 양자 시뮬레이션을 이용하면 새로운 촉매 물질을 설계하거나, 핵융합 반응을 더 효율적으로 제어할 수 있어요. 🔥
양자 광학 글을 마치며… ✍️
자, 오늘 우리는 양자 중첩을 시작으로 양자 광학의 다양한 개념들을 함께 알아봤어요. 어떠셨나요? 양자 세계는 알면 알수록 신기하고 흥미로운 것 같아요. 🤩
양자역학은 아직까지 우리에게 많은 숙제를 남겨주고 있지만, 앞으로 양자 기술이 발전하면 우리 사회에 엄청난 변화를 가져올 것이라고 믿어요. 양자 기술은 무한한 가능성을 가진 미래 기술이며, 우리 모두가 관심을 가지고 지켜봐야 할 분야랍니다. 👀
혹시 양자역학에 대해 더 궁금한 점이 있다면 언제든지 저에게 물어보세요! 제가 아는 선에서 최대한 친절하게 답변해 드릴게요. 😊 그럼 다음에 또 다른 흥미로운 주제로 만나요! 👋
양자 광학 관련 동영상







양자 광학 관련 상품검색





